NGHome

Building My Own A/B Testing Platform

Creating an A/B testing platform from scratch was a unique challenge. I wanted to build a tool capable of running both Bayesian and frequentist experiments, that provided a decent foundation to build more from, but a bit scrappy to keep it as a side project. This post walks through the development journey.

Published on 24 October 2024

Over the course of my career, I've worked across a number of projects that use external providers for A/B testing.

These tools are great, they're established, trusted and ready to go, but they can be expensive and lack a lot of flexibility that some projects end up needing further down the line. That got me thinking a couple of weeks back, I have a bit of time, I'd like to learn a bit more about how A/B testing works in the background, why not build my own platform?

And so, that's exactly what I started doing and will hopefully walk you through in this post.

Initial Requirements

As a starting point, I set out an initial list of requirements that I wanted to meet:

  • Bayesian and Frequentist A/B Testing: Supports both Bayesian and Frequentist approaches to A/B testing, providing flexibility depending on your analysis requirements.
  • Sequential Testing: Allows for running frquentist and bayesian A/B tests sequentially, stopping early if a significant result is found.
  • Bucketing: Provides functionality for bucketing users into test groups using various strategies.
  • Multiple Testing Corrections: Includes multiple testing correction algorithms such as Bonferroni, Benjamini-Hochberg, and Holm corrections.
  • Plotting: Offers built-in plotting tools for visualizing A/B test results.

Choosing the Tech Stack

To keep dependencies manageable and ensure ease of setup, I chose Poetry for dependency management and Tox for testing automation​. The CLI is built using a basic command-line interface setup, allowing users to execute tests directly from their terminals, which I found ideal for scripting automated test runs.

Additionally, I built a lightweight FastAPI framework to run the web interface, providing a way to visualize data and interact with experiments through a basic dashboard:

Web Interface

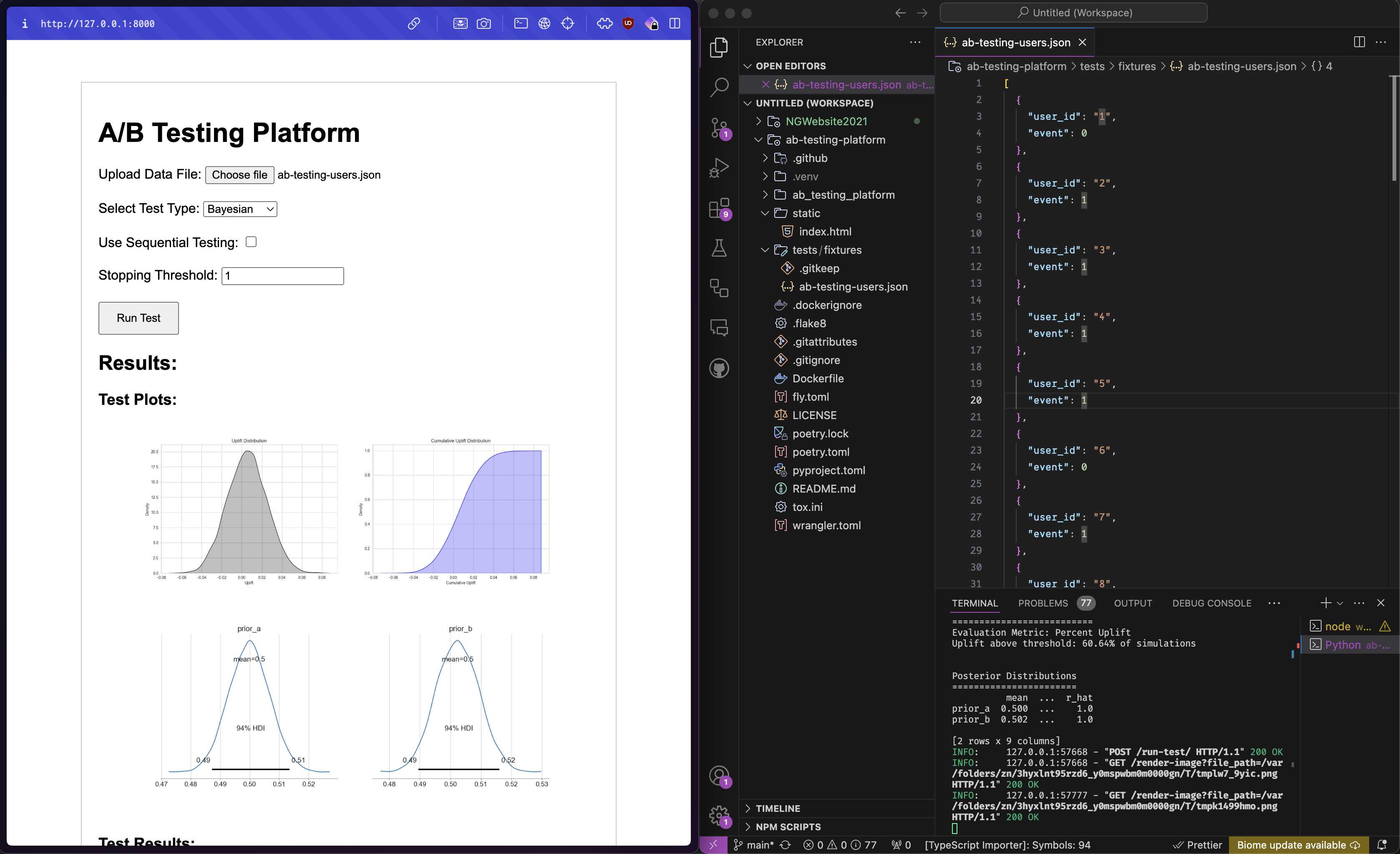A screenshot showing the initial interface on the left and a view of the app running on the right. The A/B testing platform interface, showing the initial setup and a running test.

Through the interface, users can upload a list of users and the count of conversions for the event being tracked (example).

They then select the type of test (Bayesian or Frequentist), if they want to use sequential testing and the stopping threshold for the test. They can then submit the test and will receive the results, with plots showing the test progress and outcomes shortly after.

CLI

Alongside the web interface, I also built a command line interface that allows users to take advantage of similar functionality to the web app, but from the terminal.

This is useful when running tests over scripts or alongside automated systems, which I would like to investigate more than just building a web interface (although, I may look to make this much fancier in the future).

Functionality

Bayesian and Frequentist

For this project, I wanted to start an initial implementation of both Bayesian and frequentist testing options, which allows users to choose the best method for their needs.

To implement this, I used the PyMC3 library, which has already done a lot of the heavy lifting for Bayesian testing, which I like considering I'm not big on maths.

It looks like this:

# Defining the Bayesian model using PyMC
with pm.Model() as model:
    # Priors for variant A and B (Beta distributions with prior data)
    prior_a = pm.Beta(
        "prior_a", alpha=self.prior_successes + 1, beta=self.prior_failures + 1
    )
    prior_b = pm.Beta(
        "prior_b", alpha=self.prior_successes + 1, beta=self.prior_failures + 1
    )

    # Likelihoods (Binomial distributions) based on observed data for each variant
    likelihood_a = pm.Binomial(
        "likelihood_a",
        n=variant_a_trials,
        p=prior_a,
        observed=variant_a_successes,
    )
    likelihood_b = pm.Binomial(
        "likelihood_b",
        n=variant_b_trials,
        p=prior_b,
        observed=variant_b_successes,
    )
    
    print(f"Running {'sequential' if sequential else 'non-sequential'} Bayesian A/B test")

    if sequential:
        # Burn-in and thinning parameters for MCMC
        burn_in = 100  # Ignore the first 100 samples for model stabilization
        thinning = 5  # Only keep every 5th sample to reduce autocorrelation
        for i in range(burn_in, num_samples + 1, thinning):
            trace = pm.sample(1, return_inferencedata=True, tune=0, target_accept=0.95)
            posterior_prob = (
                (trace.posterior["prior_b"] > trace.posterior["prior_a"])
                .mean()
                .item()
            )
            if posterior_prob > stopping_threshold:
                print(
                    f"Stopping early at sample {i} with posterior probability {posterior_prob:.2f}"
                )
                break
    else:
        # Sample from the posterior distribution
        trace = pm.sample(
            num_samples, 
            return_inferencedata=True, 
            target_accept=0.95, 
            tune=1000  # Increase the number of tuning steps
        )

# Calculate the uplift based on the chosen method
self.uplift_method = uplift_method
self.uplift_dist = calculate_uplift(trace, uplift_method)

# Display the results
self.plots = display_results(trace, self.uplift_dist, uplift_method)

Frequentist is the more traditional approach of the two, instead of using prior knowledge to make decisions, you start your test with a blank slate, knowing nothing and assuming nothing about either option. To make a decision, you calculate a p-value as data comes in, telling you the likelihood of seeing results if the null hypothesis is true.

For example, given a p-value 0.05, you would have 5% chance that you would see a difference as big as the one you did when there is no difference between the two options.

This can be implemented with NumPy and SciPy, so is a fair bit simpler:

import numpy as np
import scipy.stats as st


def calculate_pvalue(stat, alt_hypothesis, alpha):
    """Calculate the p-value based on the test statistic and the hypothesis type."""
    if alt_hypothesis == "one_tailed":
        return 1 - st.norm.cdf(np.abs(stat)) if stat > 0 else st.norm.cdf(stat)
    elif alt_hypothesis == "two_tailed":
        return 2 * (1 - st.norm.cdf(np.abs(stat)))


def calculate_power(
    prop_null, trials_null, trials_alt, effect_size, alpha, alt_hypothesis
):
    """Calculate the power of the test given a specific effect size."""
    se_pooled = np.sqrt(
        prop_null * (1 - prop_null) * (1 / trials_null + 1 / trials_alt)
    )
    z_alpha = (
        st.norm.ppf(1 - alpha / 2)
        if alt_hypothesis == "two_tailed"
        else st.norm.ppf(1 - alpha)
    )
    z_effect = effect_size / se_pooled
    return 1 - st.norm.cdf(z_alpha - z_effect)

def calculate_stat_pvalue(self, sequential, stopping_threshold):
    pooled_prop, se_pooled = calculate_pooled_prop_se(self)
    stat = (self.prop_alt - self.prop_null) / se_pooled

    if sequential:
        return self.perform_sequential_testing(stopping_threshold)
    else:
        pvalue = calculate_pvalue(stat, self.alt_hypothesis, self.alpha)
        return stat, pvalue

def calculate_pooled_prop_se(self):
    pooled_prop = (self.success_null + self.success_alt) / (self.trials_null + self.trials_alt)
    se_pooled = np.sqrt(
        pooled_prop * (1 - pooled_prop) * (1 / self.trials_null + 1 / self.trials_alt)
    )
    return pooled_prop, se_pooled

User Bucketing and Sequential Testing

For user bucketing, I wanted to keep things simple but also supporrt both the frequentist and bayesian approaches.

To do this, I implemented a simple function that would be given existing data from a data warehouse and then bucket users between a number of groups based on fixed percentages.

You can find the code for this here.

As you can probably see in the code examples above, I also implemented sequential testing, which is a method of A/B testing that allows you to stop a test early if you have enough data to make a decision. This can be useful if you have a lot of data and want to make a decision as soon as possible.

Multiple Testing Corrections

One key functionality for this platform is handling multiple testing scenarios. I incorporated corrections like Bonferroni and Benjamini-Hochberg to reduce the chance of false positives. This feature allows the platform to maintain accuracy when running numerous tests simultaneously—a common challenge in data-driven environments.

All the code for this can be found here.

Next Steps

At the moment, this project is completely exploratory.

I'm not a statistician, but I hope to use this as a way to understand more about the methods used behind A/B testing and how they can be used for a scalable platform. I'd also like to see how far I could take this project, potentially a fancier interface and some more advanced features.

I'll be looking to post some more updates on this project as I go, so keep an eye out for those!

Check Out the Code

If you're interested in exploring the codebase or contributing to the project, you can find the repository here. Feel free to reach out with any questions or feedback — I'm always open to collaboration and new ideas!